Het berekenen van de momentenlijn wordt gedaan om te bepalen waar het maximale inwendige moment optreedt. Nadat dit bepaald is wordt met behulp van die gegevens vaak de maximaal optredende buigspanning berekend. In de regel stel je de momentenlijn op vanuit de dwarskrachtenlijn. Dit wordt gedaan door de lijnen in de dwarskrachtenlijn te integreren. Hieronder staan een aantal voorbeelden waarmee duidelijk wordt gemaakt hoe je de momentenlijn op moet stellen. Er wordt hier verder gewerkt op de resultaten van de voorbeelden van de dwarskrachtenlijn.

Belangrijkste wetenswaardigheden van de momentenlijn.

- Voordat je de momentenlijn opsteld moet je eerst de dwarskrachtenlijn tekenen.
- De momentenlijn is de geintegreerde van de dwarskrachtenlijn.
- Aan de tip van de balk moet het inwendige moment altijd nul bedragen.
- Waar de inwendige dwarskracht minimaal is of de x-as snijd is het inwendige moment maximaal.

Momentenlijn voorbeeld 1: Een eenvoudig voorbeeld

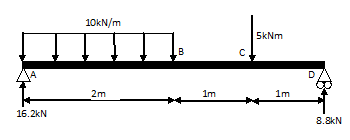
Hieronder nogmaals de situatie die we bij de dwarskrachtenlijn tegenkwamen.

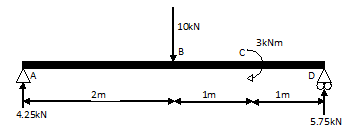
fig 1: vrije lichaams schets voorbeeld 1.

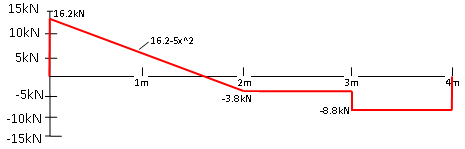
De dwarskrachtenlijn zag er als volgt uit:

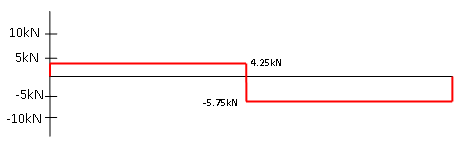
fig 2: De ingetekende dwarskrachtenlijn

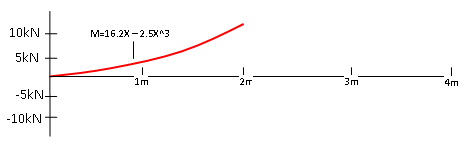
Zoals verteld moeten we nu om de momentenlijn op te stellen deze lijn integreren, dit doen we uiteraard per gedeelte. Op de eerste helft van de balk is de inwendige dwarskracht 5kN, dit is een rechte lijn en daarom is de functie hiervan; F = 4.25. Hierbij is F de inwendige dwarskracht. Deze functie moet geintegreerd worden, in dit geval is dat heel makkelijk en wordt de nieuwe functie M = 4.25X. Waarbij X de afstand over de balk is en M het inwendige moment. Deze functie geldt voor de eerste twee meter en daarom is na twee meter het inwendige moment M = 4.25 x 2 = 8.5kNm. Het eerste gedeelte van de momentenlijn is hierdoor vastgelegd en ziet er als volgt uit;

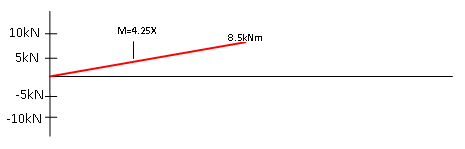
fig 3: Het eerste gedeelte van de momentenlijn

Als we vervolgens weer naar de dwarskrachtenlijn kijken dan zien we dat vanaf 2 meter de inwendige dwarskracht -5.75kN bedraagt, de functie hiervan is F = -5.75. Dit is net als hierboven makkelijk te integreren naar een functie van de momentenlijn. Echter dit keer heeft het inwendige moment al een waarde van 8.5kNm zoals te zien in figuur 3, de functie moet vanuit dat punt starten en daarom moet deze meegenomen worden in de functie nadat we deze hebben geintegreerd. De functie van de momentenlijn wordt; M = -5.75X. Als we hier de startwaarde van 8.5kNm in opnemen wordt dit; M = 8.5 - 5.75X. Als we kijken naar de dwarskrachtenlijn dan lijkt het alsof er de volgende twee meter wederom niks veranderd, maar als we goed kijken naar figuur 1 kijken bij punt C dan zie je dat daar nog een moment in staat! Dit moment is rechtsom en daarom positief, de waarde van het moment wordt bij de waarde van het huidige inwendige moment opgeteld. Tussen punt B en C zit 1 meter afstand, het inwendige moment in punt C is daarom; M = 8.5 - 5.75 x 1 = 2.75kNm. Na het optellen van het moment is dit dus 5.75kNm.

Vervolgens is de huidige inwendige dwarskracht nog steeds -5.75kN en daarom wordt deze functie gewoon doorgezet, enkel begint deze nu met een waarde van 5.75kNm. De functie vanaf punt C is dus M = 5.75 - 5.75X. Tussen punt C en D gebeurd verder niks wat ook wel moet omdat wanner we de functie invullen voor de laatste meter balk dan krijgen we M = 5.75 - 5.75*1 = 0! Hier is wederom te zien dat je aan het einde van de balk altijd een inwendig moment van 0 moet hebben.

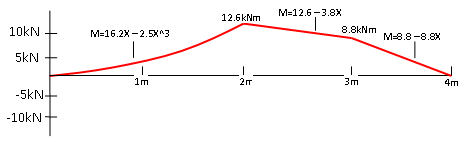
De volledig ingetekende momentenlijn ziet er nu als volgt uit;

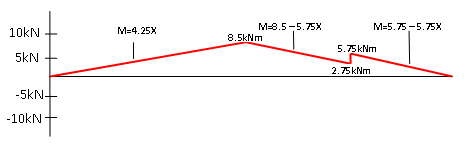
fig 4: De volledig ingetekende momentenlijn van voorbeeld 1.

Je kan nu in figuur 4 zien dat het maximale inwendige moment zich in punt B bevindt met een waarde van 8.5kNm, met dit gegeven zou je voor dit punt op de balk nu de buigspanning kunnen berekenen.

Momentenlijn voorbeeld 2: Een verdeelde belasting.

We gaan hier wederom uit van de situatie die al is uitgewerkt bij de dwarskrachtenlijn, de situatie zag er daar als volgt uit;


fig 5: vrije lichaams schets voorbeeld 2

De dwarskrachtenlijn van deze vrije lichaams schets zag er als volgt uit;


fig 6: de ingetekende dwarskrachtenlijn van voorbeeld 2.

Vanuit deze dwarskrachtenlijn gaan we nu doormiddel van te integreren de momentenlijn opstellen. Als nieuwtje heeft deze dwarskrachtenlijn een schuine lijn welke dus al een tweede graads verglijking is, als we deze nogmaals integreren krijgen we een derde graads functie en dus een lijn met een kromming erin. Dit is verder dus helemaal geen probleem. Hieronder zal ik de momentenlijn stap voor stap opstellen.

In punt A of op 0 meter begint de functie F = 16.2 - 5X^2. Deze functie moet geintegreerd worden, omdat er een - tussen de twee termen staat kunnen we deze apart integreren en vervolgens weer achter elkaar zetten. Als we dit doen dan krijgen we voor het inwendige moment de volgende functie; M = 16.2X - 2.5X^3. Deze functie geld tot punt B of tot 2 meter op de balk en zal daar een waarde hebben van M = 16.2*2 - 2.5*2^3 = 12.6kNm. De lijn ziet er als volgt uit;


fig 7: Eerste gedeelte van de momentenlijn

Als we vervolgens weer naar de dwarskrachtenlijn kijken dan zien we tussen punt B en C een rechte lijn met een waarde van F = -3.8kN, Geintegreerd wordt dit dan M = -3.8X. Omdat het inwendige moment in punt B al 12.6kNm bedraagt moeten we in dat punt beginnen en daarom wordt de functie M = 12.6 - 3.8X. De waarde van het inwendige moment in punt C is dan M = 12.6 - 3.8*1 = 8.8kNm.

Vanaf punt C tot punt D bedraagt de inwendige dwarskracht -8.8kN, Geintegreerd en met de begin waarde van 8.8 kNm wordt de functie van het inwendig moment M = 8.8 - 8.8X en dat resulteerd weer in een eindresultaat van 0!

Volledig ingetend ziet de momentenlijn er als volgt uit;

fig 8: Volledige momentenlijn voorbeeld 2

Je kan nu concluderen dat het maximale moment zicht in punt B bevindt of wel 2 meter op de balk. Hier zou nu wederom de buigspanning berekend kunnen worden.

Reageer: