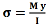Buigspanning berekenen
De buigspanning is zoals het woord zegt de spanning die in een materiaal optreedt ten gevolge van buiging. De buiging komt voort uit de inwendige krachten en momenten op een onderdeel die vaak bepaald worden met behulp van de dwarskrachtenlijn en de momentenlijn.
Belangrijkste wetenswaardigheden bij de buigspanning:
De buigspannings formule:- Ter hoogte van de neutrale lijn is de buigspanning nul.
Sigma = De buigspanning in N/mm^2.
M = Het inwendige moment in N*mm
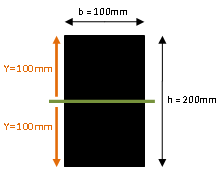
y = De afstand tot de neutrale lijn in mm.
I = Kwadratisch oppervlakte moment in mm^4.
- De buigspanning is maximaal aan de boven en/of onderzijde van het profiel.
- Het inwendige moment probeert het profiel/balk altijd om de neutrale lijn te buigen.