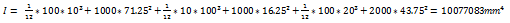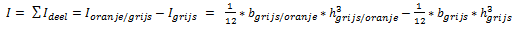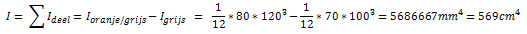Kwadratisch oppervlakte Moment
Het kwadratisch oppervlakte moment(ook wel foutief traagheidsmoment genoemd) is een waarde die ontstaat ten gevolge van de geometrische vorm in een richting van een doorsnede. Veelal de x y en z as. De waarde heeft de wordt gegeven in m^4 en wordt in verscheidene formules gebruikt zoals bij het berekenen van de buigspanning, schuifspanning en de verplaatsing. Het kwadratisch oppervlakte moment wordt aangegeven met de hoofdletter I en beschrijft de weerstand tegen buiging.(Hoe groter I, hoe groter de weerstand.)
Bij het gebruik van standaardprofielen zoals H-balken, Kokers, Buizen, Hoeklijnen etc. is de I waarde altijd al beschikbaar in de tabellen van deze profielen. Deze zijn hier te vinden.
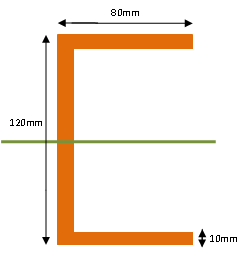
Echter zijn er altijd uitzonderingen en zelf ontworpen profielen en daarom hieronder een uitleg hoe je daarvan de I waarde kan berekenen.
Belangrijkste wetenswaardigheden van het kwadratisch oppervlakte moment:
- I waardes moeten meestal met meerdere formules bepaald worden.
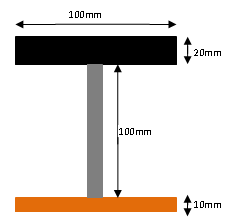
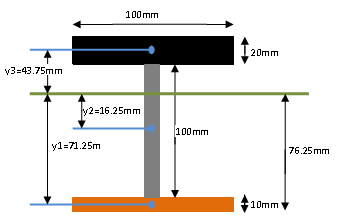
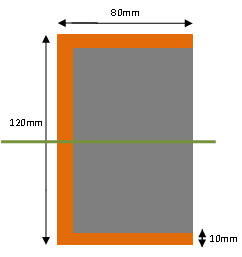
- Voor massieve rechthoekige balken geldt: I = 1/12 * b *h^3
- De hoogte van een profiel heeft vele malen meer invloed op de waarde I dan de breedte.
- Hoe groter I, hoe groter de weerstand tegen buiging.
- Afrondingen van hoeken van profielen zijn verwaarloosbaar bij de berekening.
Standaard formules voor basisvormen:
Rechthoekig oppervlak: I = 1/12 * b * h^3
Driehoekig oppervlak: I = 1/36 * b* h^3
Halfcirkelvormig oppervlak: I = 1/8 * Pi * r^4
Cirkelvormig oppervlak: I = 1/4 * Pi * r^4
Hierbij zijn; b = breedte, h = hoogte, r = straal