Het opstelleln van de dwarskrachtenlijn wordt gedaan om te bepalen waar de maximale dwarskracht optreedt. Nadat dit bepaald is wordt met behulp van die gegevens vaak de maximaal optredende schuifspanning of de momentenlijn berekend. Voordat je de dwarskrachtenlijn kan tekenen moet je eerst zorgen dat alle reactiekrachten zijn berekend en dat de vrije lichaams schets in evenwicht is.

De dwarskrachtenlijn laat voor iedere plaats op een balk zien hoe groot daar de inwendige dwarskracht is. Om duidelijk te maken hoe je een dwarskrachtenlijn maak heb ik een aantal voorbeelden gemaakt.

Belangrijkste wetenswaardigheden van de dwarskrachtenlijn.

- Voordat je de dwarskrachtenlijn tekend moeten eerst alle reactiekrachten berekend zijn.
- Aan het einde van de balk moet de inwendige dwarskracht altijd op nul uitkomen.
- Momenten die in de vrije lichaams schets staan hebben geen invloed op de dwarskrachtenlijn.

Dwarskrachtenlijn voorbeeld 1: Een eenvoudig voorbeeld

Hieronder een simpele situatie van een balk welke op twee punten is ondersteund en waar de reactiekrachten al bekend zijn.

fig 1: vrije lichaams schets voorbeeld 1.

Bij het tekenenen van de dwarskrachtenlijn begin je altijd helemaal links of helemaal recht. De meeste mensen(waaronder ik) beginnen altijd links en zo zullen de voorbeelden ook worden behandeld. Als we kijken aan het begin van de balk bij scharnierpunt A dan is hier een kracht van 4.25kN te vinden, dit is de start van de dwarskrachtenlijn. Als we vervolgens een meter naar rechts gaan dan is er nog niks veranderd en daarom is daar de inwendige dwarskracht nog steeds 4.25kN.

Als we vervolgens nog een meter naar rechts gaan dan kom je bij punt B en daar staat een kracht van 10kN naar beneden. De huidige inwendige dwarskracht is 4.2kN, de nieuwe inwendige dwarskracht wordt dan 4.25kN - 10kN = -5.75kN. Vervolgens gaan we weer verder naar rechts tot punt C en daar vinden we een moment van 3kNm. Hier hoeven we echter helemaal niks mee te doen omdat we hier een DWARSKRACHTEN lijn aan het tekenenen zijn. We gaan dus gewoon weer verder tot punt D, daar zien we wederom een omhoog gerichte kracht van 5kN. De nieuwe inwendige dwarskracht wordt dus -5.75kN + 5.75kN = 0kN! Dit brengt ons gelijk tot een belangrijke regel bij het tekenen van de dwarskrachtenlijn en dat is dat aan het einde van de balk de inwendige dwarskracht altijd nul moet zijn! Als dit niet zo is dan zijn of de reactiekrachten niet goed berekend of je moet je dwarskrachtenlijn nogmaals nakijken.

Als we de berekende waardes nu intekenen in een grafiek dan krijgen we de volgende dwarskrachtenlijn:

fig 2: De ingetekende dwarskrachtenlijn

Te zien is dat de maximaal optredende dwarskracht -5.75kN bedraagt, met dat gegeven zou je nu de schuifspanning kunnen bepalen of van met behulp van de dwarskrachtenlijn de momentenlijn kunnen opstellen om de maximale buigspanning te bepalen.

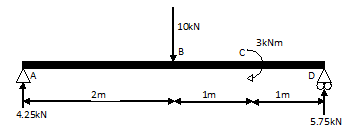
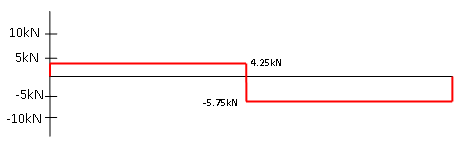
Dwarskrachtenlijn voorbeeld 2: Een verdeelde belasting.

Op een balk kan natuurlijk ook een verdeelde belasting worden uitgeoefend. Je heb hier verschillende varianten in, men heeft de gelijkmatig verdeelde belasting en de ongelijkmatig verdeelde belasting. In beide gevallen moet er geintegreerd worden om de dwarskrachtenlijn op te stellen. Nu hoef je daar niet van te schrikken want het gaat veelal om de meest simpele integralen.

We zullen opnieuw doormiddel van het onderstaande voorbeeld duidelijk maken hoe het in zijn werking gaat, Hier zijn de reactiekrachten ook al berekend.

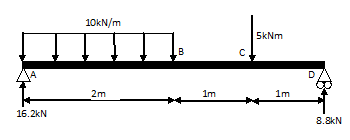
fig 3: vrije lichaams schets voorbeeld 2

We beginnen weer links bij punt A. Hier vinden we een omhoog gerichte kracht van 16.2kN, ook begint hier de verdeelde belasting maar omdat dit een belasting per meter is stelt deze op punt 0 nog niks voor. Om dat even duidelijk te maken het volgende stukje tekst:

Stel je heb een verdeelde belasting van 10kN per meter, dan betenend dit dat wanneer deze belasting een meter lang is de totale belasting 10kN bedraagt. Als de belasting 2 meter lang is dan is de totale belasting 10kN x 2 = 20kN. Als de belasting 0.5 meter lang is dan is de totale belasting 10 x 0.5 = 5kN. En dan als laatst bij een lengte van 0 meter is de totale belasting 10kN x 0 = 0kN!

Omdat in punt A van het voorbeeld de verdeelde belasting net begint is de lengte op dat moment ook 0 meter en daarom heeft deze nog geen waarde!

We beginnen dus met een omhoog gerichte belasting van 16.2kN. Als we vervolgens wat verder gaan dan zal de totale belasting van de verdeelde belasting langzaam aan al meer worden. Je kan dan natuurlijk voor ieder plekje opnieuw de dwarskracht berekenen of je kan de functie van de dwarskracht ook even integreren en dat is wat we hier zullen doen.
De verdeelde belasting is constant en daarom is de functie hiervan; F = 10X, hierbij is F de totale dwarskracht en X de plaats op de balk. Als we deze functie integreren dan krijgen we F = 5Xˆ2, Als je niet weet hoe dit moet kijk dan bij de standaard integralen op deze website! Omdat we in punt A al een positieve dwarskracht van 16.2kN hebben moet de functie in dit punt beginnen, daarom wordt de functie; F = 16.2 - 5Xˆ2. Let hierbij goed op het minteken want de belasting is naar beneden gericht! De functie wordt net zolang doorgetrokken tot waar de belasting eindigd en dat is twee meter verder in punt B, de inwendige dwarskracht is daar dan F = 16.2 - 5 x 2ˆ2 = -3.8kN

De dwarskrachtenlijn is nu al bekend tot vlak na de verdeelde belasting en ziet er als volgt uit;

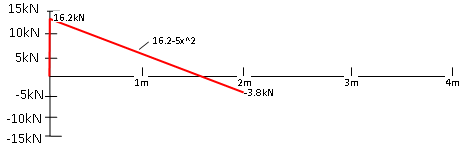
fig 4: Ingetekende verdeelde belasting

Omdat er de tussen punt B en C niks gebeurt blijft de lijn ook gewoon constant tot punt C. In punt C zien we een normale dwarskracht die naar beneden is gericht, deze wordt dus direct van de huidige waarde van de lijn afgetrokken, hierdoor wordt de inwendige dwarskracht vanaf dat punt -3.8 - 5 = -8.8kN. Als we vervolgens verder gaan naar punt D dan zien we een omhoog gerichtte kracht van 8.8kN en hierdoor wordt de inwendige dwarskracht aan het einde van de balk 0, wat betekend dat we het goed hebben gedaan!

De totale dwarskrachtenlijn ziet er dan als volgt uit;

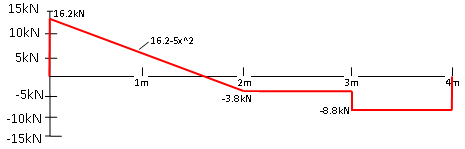
fig 5: volledig ingetekende dwarskrachtenlijn voorbeeld 2.

Reageer: